‍

‍

Every time you get accurate Netflix recommendations, your smartphone recognizes your voice, or an autonomous car safely navigates traffic, loss functions in machine learning are working behind the scenes. These mathematical powerhouses serve as the compass that guides AI models toward making better predictions by measuring the gap between what a model predicts and what actually happens.

What Are Loss Functions in Machine Learning?

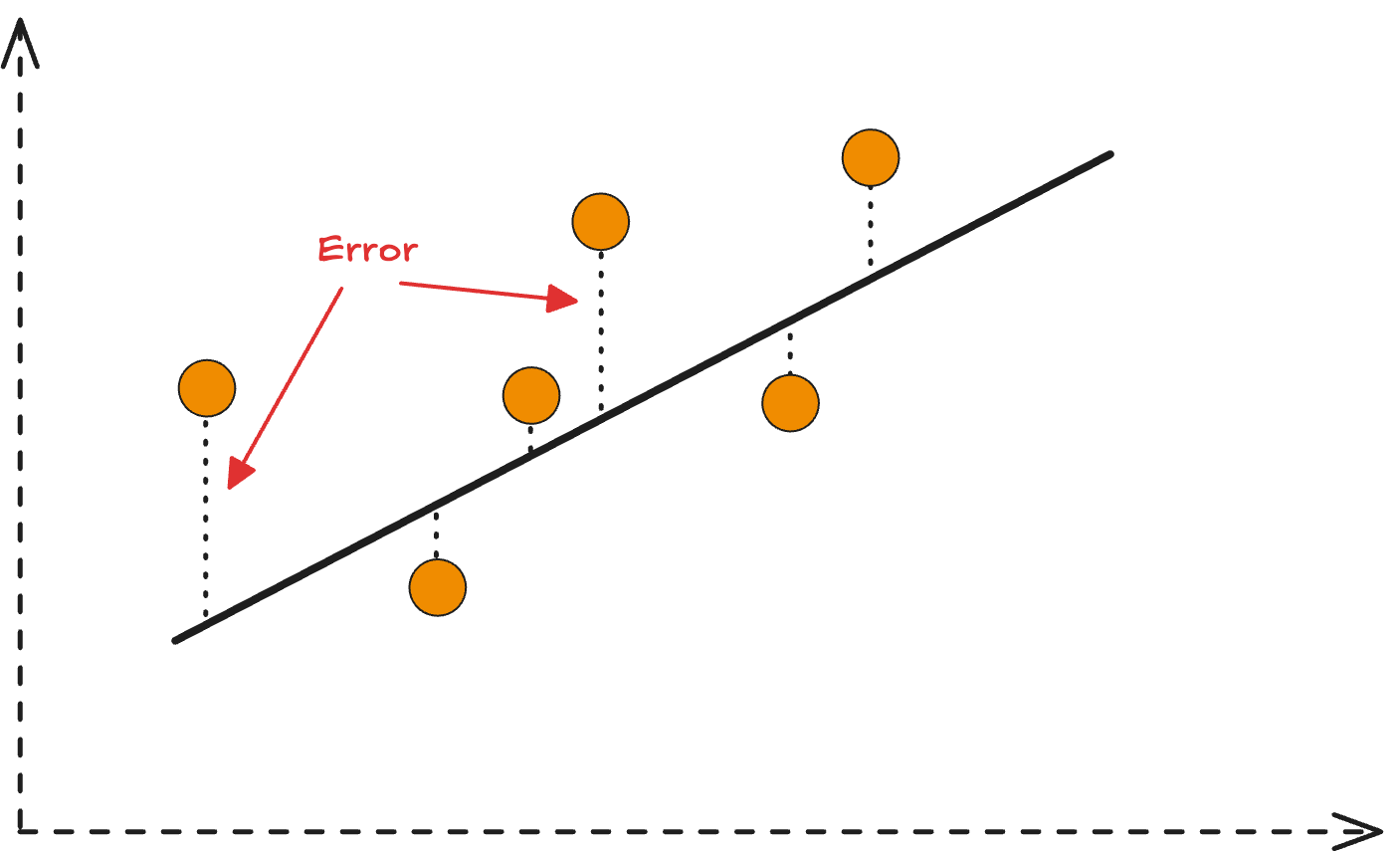
Loss functions are mathematical formulas that quantify how far off a machine learning model's predictions are from the actual target values. Think of them as scorekeepers in the world of AI—they tell optimization algorithms exactly how wrong the model is and in which direction to improve.

The Mathematical Foundation of Loss Functions

At its core, a loss function transforms the abstract concept of "model accuracy" into concrete numbers that computers can work with. The fundamental goal is simple: minimize the loss to maximize model performance.

Key Components:

• Individual loss: Error calculation for single predictions
• Cost function: Average loss across entire training datasets
• Gradient generation: Directional guidance for parameter updates
• Optimization feedback: Critical input for learning algorithms

This mathematical framework enables neural networks and other machine learning algorithms to learn systematically from data.

Why Loss Functions Matter in Deep Learning

Loss functions serve as the critical bridge between model predictions and the optimization process. During neural network training, models make predictions, loss functions evaluate accuracy, and this evaluation generates gradients that guide parameter adjustments.

The Training Feedback Loop

The iterative machine learning training process relies on this essential feedback mechanism:

1. Model prediction: Neural network generates output
2. Loss calculation: Function measures prediction accuracy
3. Gradient computation: Determines parameter adjustment direction
4. Weight updates: Optimizer improves model parameters
5. Repeat: Process continues until convergence

Without loss functions, AI models would lack the directional guidance necessary for systematic improvement.

Regression Loss Functions: Predicting Continuous Values

Mean Squared Error (MSE): The Foundation

Mean Squared Error (MSE) is the most fundamental regression loss function for predicting continuous values like house prices, stock prices, or temperature forecasts.

MSE Formula:

MSE = (1/n) × Σ(actual - predicted)²

MSE Advantages and Applications

• Gradient-friendly: Smooth derivatives enable stable optimization
• Penalizes large errors: Squared terms emphasize significant mistakes
• Computationally efficient: Simple calculation for large datasets
• Standard benchmark: Widely used baseline for regression tasks

Real-World MSE Applications:

• Financial forecasting: Predicting stock prices and market trends
• Weather prediction: Temperature and precipitation forecasting
• Sales forecasting: Revenue and demand prediction models
• Medical diagnosis: Continuous biomarker prediction

Mean Absolute Error (MAE): Robust to Outliers

Mean Absolute Error (MAE) provides an alternative regression loss function that's more robust to outliers than MSE.

MAE Benefits:

• Outlier resistance: Linear treatment of all errors
• Interpretable: Direct average of absolute differences
• Balanced sensitivity: Equal weight to all prediction errors
• Robust optimization: Stable gradients for diverse datasets

Industry Applications:

• Supply chain optimization: Inventory and logistics forecasting
• Energy management: Power consumption prediction
• Healthcare analytics: Patient outcome forecasting with noisy data

Huber Loss: Best of Both Worlds

Huber loss combines MSE and MAE advantages, providing a hybrid approach for robust machine learning:

• Small errors: Behaves like MSE for precise optimization
• Large errors: Transitions to MAE behavior for outlier resistance
• Adaptive sensitivity: Adjusts behavior based on error magnitude
• Stable training: Maintains gradient flow in deep neural networks

Classification Loss Functions: Predicting Categories

Binary Cross-Entropy Loss: Two-Class Problems

Binary cross-entropy loss is the gold standard for binary classification tasks like spam detection, medical diagnosis, or fraud detection.

Mathematical Formula:

BCE = -[y×log(p) + (1-y)×log(1-p)]

Binary Cross-Entropy Applications

Key Advantages:

• Probability calibration: Outputs well-calibrated probabilities
• Strong gradients: Provides clear optimization signals
• Sigmoid compatibility: Works perfectly with sigmoid activation
• Interpretable outputs: Direct probability interpretation

Real-World Binary Classification:

• Email security: Spam vs. legitimate email detection
• Medical screening: Disease presence/absence prediction
• Credit scoring: Loan approval/rejection systems
• Fraud detection: Transaction legitimacy assessment

Categorical Cross-Entropy: Multi-Class Classification

Categorical cross-entropy loss extends binary classification to multiple classes, essential for multi-class classification problems.

Use Cases and Benefits:

• Image recognition: Classifying objects into multiple categories
• Natural language processing: Sentiment analysis with multiple emotions
• Recommendation systems: Predicting user preferences across categories
• Computer vision: Medical image classification into multiple conditions

Industry Applications:

• E-commerce: Product categorization and recommendation
• Social media: Content classification and moderation
• Autonomous vehicles: Object detection and classification
• Healthcare: Multi-disease diagnosis from medical imaging

Hinge Loss: Maximum Margin Classification

Hinge loss focuses on creating robust decision boundaries, originally popularized by Support Vector Machines but now used in neural networks.

Hinge Loss Benefits:

• Margin maximization: Creates robust decision boundaries
• Sparsity promotion: Focuses on difficult examples near boundaries
• Computational efficiency: Simple calculation for large datasets
• Robust classification: Handles noisy data effectively

Advanced Loss Function Concepts

Regularization in Loss Functions

Regularized loss functions prevent overfitting by adding penalty terms that discourage model complexity:

L1 Regularization (Lasso)

• Feature selection: Promotes sparse models
• Automatic variable selection: Reduces irrelevant features
• Interpretability: Creates simpler, more understandable models

L2 Regularization (Ridge)

• Weight decay: Prevents extremely large parameters
• Smooth solutions: Encourages balanced feature usage
• Numerical stability: Improves optimization convergence

Regularized Loss Formula:

L_regularized = L_original + λ × R(parameters)

Where λ controls regularization strength and R represents the penalty term.

Choosing the Right Loss Function: Decision Guide

Data-Driven Selection Criteria

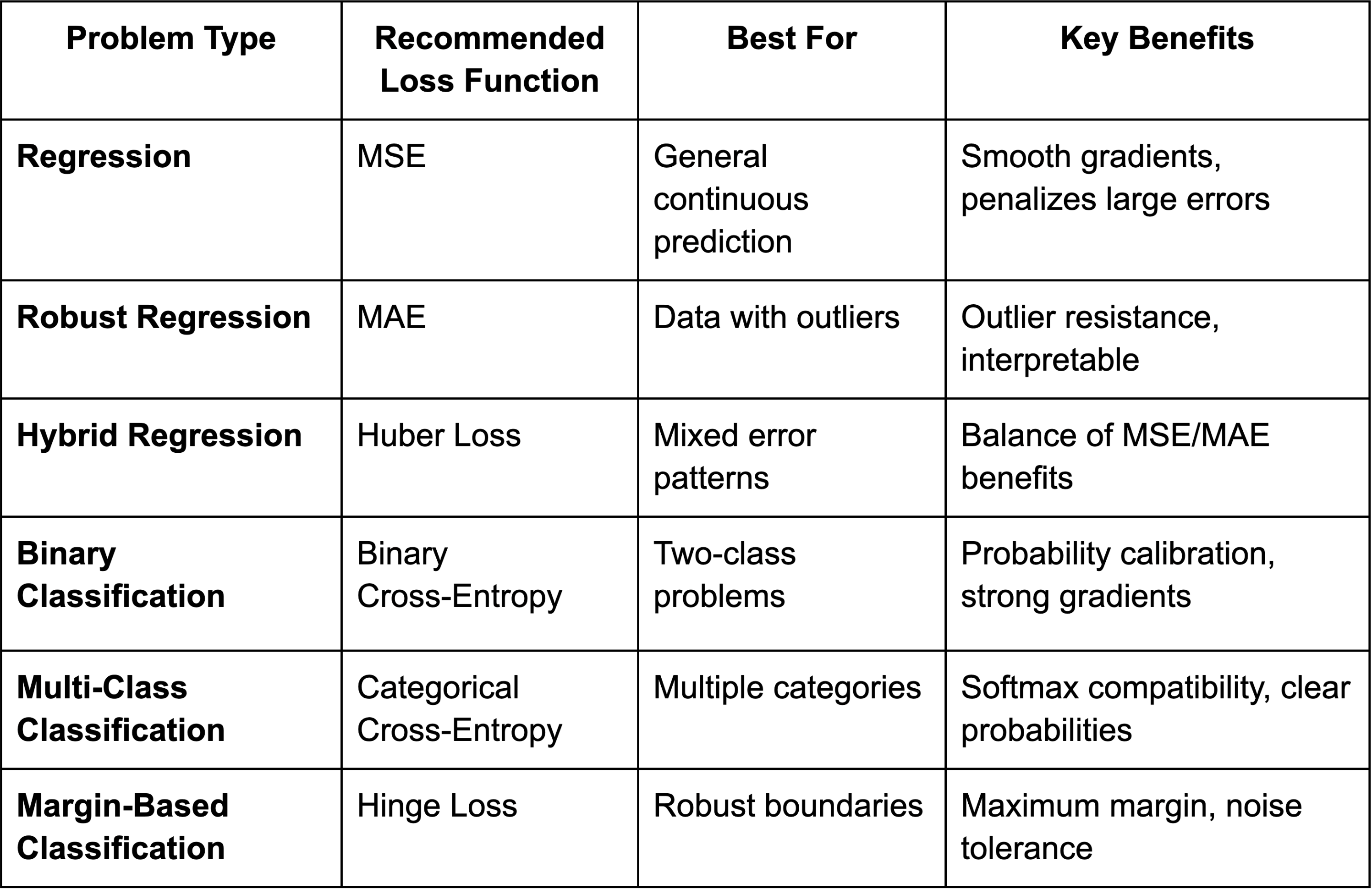
Dataset Characteristics:

• Outlier presence: Choose MAE or Huber for robust handling
• Class imbalance: Consider weighted loss functions
• Noise levels: Robust losses for noisy data
• Dataset size: Simple losses for large-scale training

Model Requirements:

• Probability outputs: Cross-entropy for calibrated probabilities
• Feature selection: L1-regularized losses for sparsity
• Computational constraints: Simple losses for efficiency
• Interpretability needs: MAE for direct error interpretation

Loss Functions in Modern Deep Learning

Custom Loss Functions for Specialized Tasks

Modern AI applications often require custom loss functions tailored to specific objectives:

Domain-Specific Examples:

• Computer vision: Perceptual loss for image generation quality
• Recommendation systems: Ranking loss for personalized suggestions
• Generative AI: Adversarial loss for realistic content creation
• Medical AI: Focal loss for rare disease detection

Loss Landscape Optimization

Loss landscapes—how loss values change across parameter space—critically impact neural network training:

Landscape Properties:

• Smoothness: Enables stable gradient descent
• Convexity: Guarantees global optima (rare in deep learning)
• Local minima: Multiple optimal solutions in complex models
• Saddle points: Training challenges in high-dimensional spaces

Numerical Stability in Practice

Production loss functions must handle numerical edge cases:

Implementation Considerations:

• Logarithm stability: Clip inputs to prevent infinite values
• Exponential overflow: Use numerical tricks for large values
• Gradient clipping: Prevent exploding gradients
• Mixed-precision training: Maintain accuracy with efficiency

Monitoring Loss Functions During Training

Loss Curve Analysis

Training loss patterns reveal critical insights about model performance:

Healthy Training Patterns:

• Decreasing loss: Consistent improvement over epochs
• Convergence: Loss stabilization at optimal values
• Smooth curves: Stable optimization without oscillations

Warning Signs:

• Increasing loss: Potential overfitting or learning rate issues
• Oscillating loss: Unstable optimization requiring adjustment
• Plateauing loss: Need for learning rate decay or architecture changes

Validation Loss Monitoring

Validation loss tracking prevents overfitting and ensures generalization:

• Early stopping: Halt training when validation loss increases
• Hyperparameter tuning: Optimize based on validation performance
• Model selection: Choose architectures with best validation scores
• Regularization adjustment: Balance training and validation performance

Emerging Trends in Loss Function Design

Adaptive and Learned Loss Functions

Next-generation loss functions adapt to data characteristics automatically:

Research Directions:

• Meta-learning losses: Automatically discover optimal functions
• Curriculum learning: Gradually increase loss complexity
• Dynamic weighting: Adjust loss components during training
• Adversarial losses: Competitive training for improved robustness

Multi-Objective Optimization

Modern applications often require balancing multiple objectives:

Multi-Objective Approaches:

• Weighted combinations: Balance accuracy, fairness, and efficiency
• Pareto optimization: Find optimal trade-offs between objectives
• Hierarchical losses: Priority-based objective optimization
• Constraint incorporation: Hard constraints within loss functions

Best Practices for Loss Function Implementation

Production Deployment Considerations

Real-world loss function deployment requires careful engineering:

Performance Optimization:

• Vectorized computation: Leverage GPU acceleration
• Batch processing: Efficient large-scale calculation
• Memory management: Optimize for large dataset training
• Gradient checkpointing: Balance memory and computation

Monitoring and Debugging:

• Loss visualization: Track training progress effectively
• Gradient analysis: Detect vanishing/exploding gradients
• Statistical monitoring: Detect distribution shifts in production
• A/B testing: Compare loss function performance empirically

Future of Loss Functions in AI

Quantum and Neuromorphic Computing

Emerging computing paradigms will influence loss function design:

• Quantum loss functions: Leverage quantum superposition for optimization
• Neuromorphic losses: Mimic biological learning mechanisms
• Energy-efficient losses: Optimize for low-power edge computing
• Federated losses: Privacy-preserving distributed optimization

Integration with Human Feedback

Human-in-the-loop learning incorporates human preferences directly into loss functions:

• Reinforcement learning from human feedback (RLHF): Used in ChatGPT and similar models
• Preference learning: Optimize based on human choice data
• Interactive optimization: Real-time loss adjustment based on feedback
• Ethical constraints: Incorporate fairness and safety into loss design

Conclusion: Mastering Loss Functions for Better AI

Loss functions are the mathematical engines that transform human objectives into algorithmic optimization targets. From fundamental MSE regression to sophisticated multi-objective optimization, these functions determine how effectively AI models learn from data.

Understanding loss function selection, implementation, and monitoring is crucial for developing robust machine learning systems. Whether you're building computer vision models, natural language processing systems, or recommendation engines, choosing the right loss function significantly impacts model performance and business outcomes.

‍