Meta Description: Master the backpropagation algorithm: how neural networks learn through gradient descent, chain rule, and error propagation. Complete guide with examples and implementations.

‍

Every time ChatGPT understands your questions, your smartphone recognizes your face, or Netflix recommends the perfect show, the backpropagation algorithm is working behind the scenes. This mathematical breakthrough is the engine that enables neural networks to learn from mistakes and continuously improve their predictions. Without backpropagation, modern AI as we know it simply wouldn't exist.

What Is the Backpropagation Algorithm?

Backpropagation (short for "backward propagation of error") is the fundamental algorithm that trains artificial neural networks by systematically adjusting their internal parameters based on prediction errors. Think of it as a teacher that shows a neural network exactly how wrong it was and precisely how to improve.

The Core Innovation of Backpropagation

The backpropagation algorithm solves one of the most challenging problems in machine learning: how to efficiently compute gradients for millions or billions of parameters in deep neural networks. By leveraging the mathematical chain rule, backpropagation transforms this seemingly impossible optimization problem into a manageable computational process.

Key Components:

• Error measurement: Quantifies how wrong predictions are
• Gradient computation: Calculates adjustment directions for each parameter
• Parameter updates: Systematically improves network weights and biases
• Iterative learning: Repeats the process until optimal performance

This elegant approach enables neural networks to learn complex patterns from data automatically.

How Backpropagation Works: The Complete Process

Step 1: Forward Pass - Making Predictions

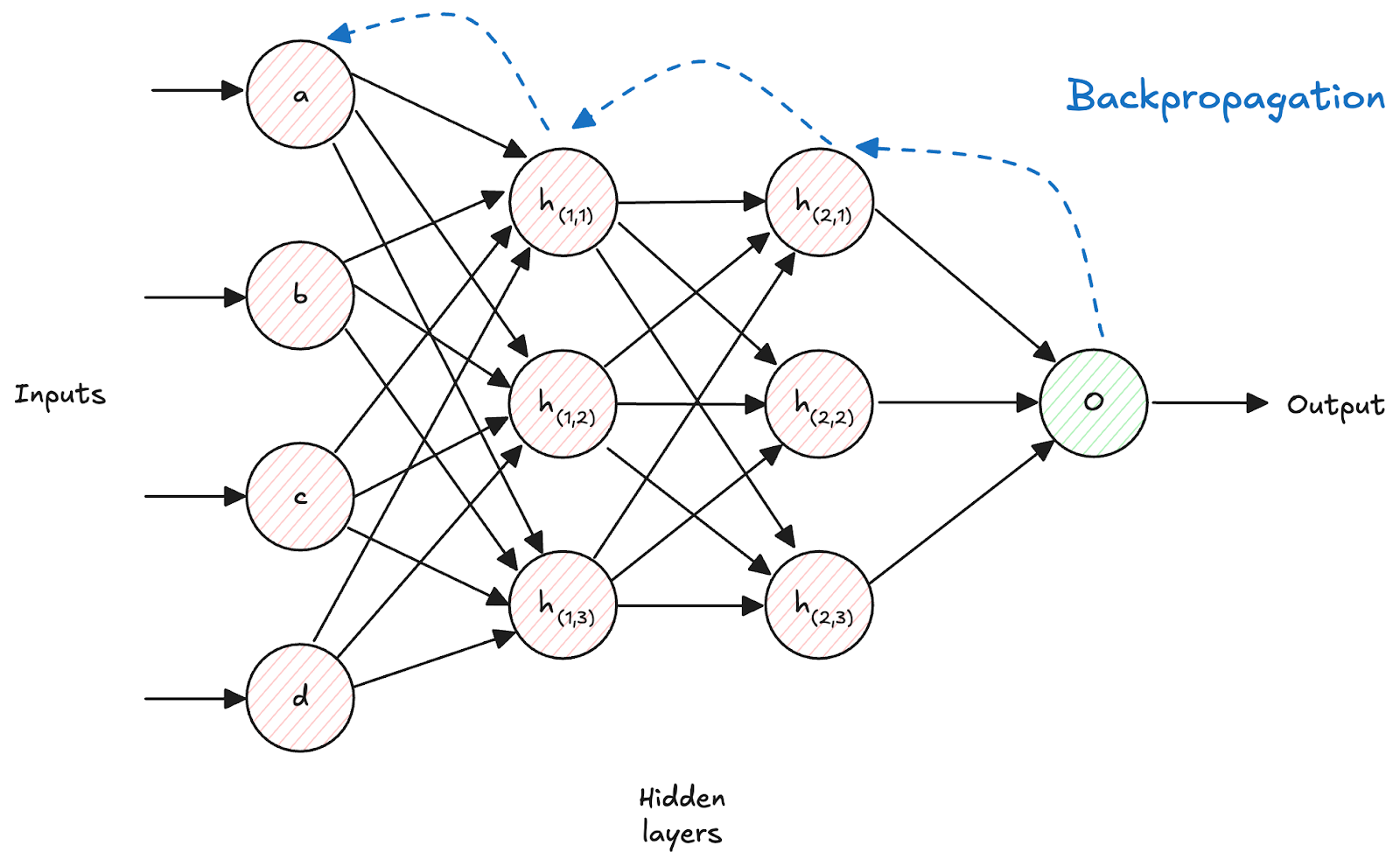
The backpropagation process begins with a forward pass through the neural network. Input data flows through successive layers, with each layer applying mathematical transformations to gradually extract meaningful features and generate predictions.

Forward Pass Components:

• Linear transformations: Matrix multiplications with learned weights
• Bias additions: Learned offset values for better fitting
• Activation functions: Nonlinear transformations (ReLU, sigmoid, tanh)
• Layer-by-layer processing: Progressive feature extraction

Mathematical Formula:

activation_layer = activation_function(weights × input + bias)

Real-World Example: In image recognition, early layers detect edges, middle layers identify shapes, and final layers recognize complete objects like cats or dogs.

Step 2: Loss Calculation - Measuring Errors

After generating predictions, the algorithm calculates how far off the predictions are using a loss function. This error measurement provides the critical feedback needed for learning.

Common Loss Functions:

• Mean Squared Error: For regression tasks like price prediction
• Cross-Entropy Loss: For classification tasks like image recognition
• Custom Loss Functions: For specialized applications like recommendation systems

Step 3: Backward Pass - The Magic of Learning

The backward pass represents the core innovation of backpropagation. Starting from the output layer, the algorithm computes gradients by working backwards through the network using the chain rule of calculus.

Backward Pass Process:

• Output layer gradients: Direct computation from loss function
• Hidden layer gradients: Chain rule application through network layers
• Weight gradients: How each parameter affects the overall error
• Bias gradients: Adjustment directions for bias parameters

Mathematical Foundation: The chain rule enables decomposing complex derivatives into manageable local computations:

∂Loss/∂Weight = ∂Loss/∂Output × ∂Output/∂Activation × ∂Activation/∂Weight

Step 4: Parameter Updates - Learning from Mistakes

Once gradients are computed, the algorithm updates all network parameters using optimization algorithms like gradient descent:

Update Formula:

new_weight = old_weight - learning_rate × gradient

Key Factors:

• Learning rate: Controls step size during optimization
• Gradient magnitude: Indicates strength of required adjustment
• Momentum: Helps accelerate convergence and avoid local minima
• Regularization: Prevents overfitting through parameter constraints

The Mathematical Foundation: Chain Rule in Action

Understanding the Chain Rule for Neural Networks

The chain rule of calculus is the mathematical principle that makes backpropagation possible. It allows computing how changes in any network parameter affect the final prediction error.

Chain Rule Principle: If you have a composite function f(g(x)), the derivative is:

df/dx = df/dg × dg/dx

Applying Chain Rule to Deep Networks

For deep neural networks with multiple layers, the chain rule extends naturally:

Multi-Layer Gradient Computation:

• Layer-by-layer decomposition: Break complex derivatives into simple parts
• Gradient accumulation: Combine effects across all network paths
• Efficient recomputation: Store intermediate results for computational efficiency
• Automatic differentiation: Modern frameworks handle this automatically

Industry Applications:

• Computer vision: Training CNNs for medical image analysis
• Natural language processing: Training transformers for language translation
• Speech recognition: Training RNNs for voice assistants
• Recommendation systems: Training collaborative filtering models

Backpropagation Algorithm Variants and Extensions

Batch Backpropagation vs. Online Learning

Batch Processing:

• Full dataset processing: Computes gradients using entire training set
• Stable convergence: Smoother optimization with less noise
• Memory intensive: Requires storing large amounts of data
• Parallel computation: Leverages modern GPU architectures effectively

Online Learning:

• Individual example processing: Updates parameters after each training sample
• Fast adaptation: Quick response to changing data patterns
• Memory efficient: Processes one sample at a time
• Noisy gradients: Can help escape local minima but less stable

Mini-Batch Backpropagation: Best of Both Worlds

Mini-batch learning strikes the optimal balance between computational efficiency and gradient stability:

Advantages:

• Computational efficiency: Leverages parallel processing capabilities
• Gradient stability: Reduces noise compared to online learning
• Memory management: Processes manageable data chunks
• Convergence properties: Often provides fastest and most reliable training

Optimal Batch Sizes:

• Small batches (32-128): Better for noisy datasets and limited memory
• Medium batches (256-512): General-purpose training for most applications
• Large batches (1024+): High-performance computing with massive datasets

Common Challenges in Backpropagation Implementation

Gradient Explosion: When Learning Goes Wrong

Exploding gradients cause unstable training where parameter updates become extremely large, leading to divergent behavior.

Prevention Strategies:

• Gradient clipping: Limit maximum gradient magnitude
• Learning rate scheduling: Adaptive reduction during training
• Batch normalization: Normalize inputs to each layer
• Proper initialization: Start with appropriate weight distributions

Memory and Computational Challenges

Modern deep learning requires managing substantial computational resources:

Memory Optimization Techniques:

• Gradient checkpointing: Trade computation for memory efficiency
• Mixed-precision training: Use 16-bit floats to reduce memory usage
• Model parallelism: Distribute large models across multiple devices
• Data parallelism: Process different batches on separate GPUs

Advanced Backpropagation Applications

Convolutional Neural Networks (CNNs)

CNNs use specialized backpropagation that accounts for weight sharing and spatial structure:

CNN-Specific Considerations:

• Weight sharing: Gradients accumulated across all spatial positions
• Convolution operations: Specialized gradient computation for filters
• Pooling layers: Gradient routing through downsampling operations
• Spatial relationships: Maintaining local connectivity patterns

Real-World CNN Applications:

• Medical imaging: Diagnosing diseases from X-rays and MRIs
• Autonomous vehicles: Object detection and scene understanding
• Manufacturing: Quality control through visual inspection
• Agriculture: Crop monitoring and disease detection

Recurrent Neural Networks (RNNs)

RNNs require backpropagation through time (BPTT), extending standard backpropagation to handle sequential data:

BPTT Process:

• Temporal unrolling: Expand recurrent connections across time steps
• Gradient accumulation: Sum gradients across all time steps
• Memory considerations: Store activations for entire sequences
• Truncated BPTT: Limit gradient propagation for computational efficiency

Sequential Data Applications:

• Language modeling: Training GPT and similar text generation models
• Machine translation: Converting between different languages
• Speech recognition: Converting audio to text transcriptions
• Time series forecasting: Predicting stock prices and weather patterns

Transformer Networks and Attention Mechanisms

Modern transformer architectures rely on backpropagation through complex attention mechanisms:

Attention Backpropagation:

• Multi-head attention: Parallel gradient computation across attention heads
• Positional encoding: Gradient flow through position embeddings
• Layer normalization: Specialized normalization gradient computation
• Feed-forward networks: Standard backpropagation within transformer blocks

Transformer Applications:

• Large language models: ChatGPT, GPT-4, and similar conversational AI
• Machine translation: Google Translate and similar services
• Code generation: GitHub Copilot and programming assistants
• Scientific research: Protein structure prediction and drug discovery

Best Practices for Backpropagation Implementation

Hyperparameter Optimization

Successful backpropagation requires careful tuning of key hyperparameters:

Critical Hyperparameters:

• Learning rate: Controls optimization step size (typically 0.001-0.1)
• Batch size: Balances computational efficiency and gradient quality
• Network architecture: Number of layers and neurons per layer
• Regularization strength: Prevents overfitting through parameter penalties

Monitoring and Debugging Training

Effective training requires continuous monitoring of key metrics:

Essential Monitoring Metrics:

• Training loss: Should decrease consistently over time
• Validation loss: Indicates generalization performance and overfitting
• Gradient norms: Detect vanishing/exploding gradient problems
• Learning curves: Visualize training progress and convergence

Debugging Techniques:

• Gradient checking: Verify gradient computation accuracy numerically
• Activation visualization: Monitor internal network representations
• Weight histograms: Track parameter distribution changes
• Learning rate experiments: Find optimal optimization schedules

Modern Implementation Frameworks

Contemporary deep learning frameworks provide automatic backpropagation implementation:

Popular Frameworks:

• PyTorch: Dynamic computational graphs with eager execution
• TensorFlow: Static and dynamic graph support with optimization
• JAX: Functional programming approach with automatic differentiation
• Keras: High-level API for rapid prototyping and deployment

Framework Advantages:

• Automatic differentiation: No manual gradient derivation required
• GPU acceleration: Efficient parallel computation on modern hardware
• Memory optimization: Built-in techniques for large-scale training
• Debugging tools: Integrated monitoring and visualization capabilities

‍

Meta-Learning and Automated Architecture Design

Automated machine learning applies backpropagation to optimize learning algorithms themselves:

Meta-Learning Applications:

• Neural architecture search: Automatically design optimal network structures
• Hyperparameter optimization: Learn optimal training configurations
• Few-shot learning: Rapidly adapt to new tasks with minimal data
• Continual learning: Avoid catastrophic forgetting in sequential tasks

Practical Implementation Guide

Getting Started with Backpropagation

Beginners should follow this structured approach to understanding and implementing backpropagation:

Step-by-Step Learning Path:

1. Mathematical foundation: Study calculus chain rule and derivatives
2. Simple implementation: Code basic backpropagation for small networks
3. Framework usage: Learn PyTorch or TensorFlow for practical applications
4. Problem application: Apply to real datasets and evaluate performance
5. Advanced techniques: Explore regularization, optimization, and debugging

Code Example: Basic Backpropagation Structure

‍

# Simplified backpropagation implementation concept

class NeuralNetwork:

    def forward_pass(self, input_data):

        # Compute predictions layer by layer

        return predictions

    def compute_loss(self, predictions, targets):

        # Calculate error using loss function

        return loss_value

    def backward_pass(self, loss):

        # Compute gradients using chain rule

        return gradients

    def update_parameters(self, gradients, learning_rate):

        # Update weights and biases

        self.weights -= learning_rate * gradients

Performance Optimization Tips

Production deployment of backpropagation requires optimization:

Optimization Strategies:

• Vectorization: Use matrix operations instead of loops
• Memory management: Implement gradient checkpointing for large models
• Parallel processing: Leverage multiple GPUs for data parallelism
• Mixed precision: Use FP16 arithmetic for speed without accuracy loss

Conclusion: Mastering the Engine of Deep Learning

Backpropagation represents one of the most significant algorithmic breakthroughs in artificial intelligence, enabling the training of sophisticated neural networks that power modern AI applications. Its elegant combination of mathematical rigor, computational efficiency, and broad applicability makes it the foundation of deep learning.

Understanding backpropagation is essential for anyone working with neural networks and machine learning. From the mathematical principles of the chain rule to practical implementation considerations, this algorithm transforms the complex optimization problem of neural network training into a tractable computational process.

Despite challenges like vanishing gradients and computational requirements, backpropagation continues serving as the cornerstone of neural network training. Modern extensions, optimizations, and supporting techniques have addressed many limitations while preserving the algorithm's core advantages.

As artificial intelligence systems become increasingly sophisticated, backpropagation remains central to their development. Whether you're building computer vision models, natural language processing systems, or recommendation engines, mastering backpropagation is crucial for developing effective AI solutions.

Ready to implement backpropagation? Start with simple networks using modern frameworks like PyTorch or TensorFlow, focus on understanding the forward and backward passes, and gradually tackle more complex architectures as your understanding deepens. Monitor your training metrics carefully and experiment with different optimization techniques to achieve optimal performance.

The future of AI depends on continued refinement and innovation in backpropagation-based training methods. Understanding this fundamental algorithm positions you to contribute to the next generation of artificial intelligence breakthroughs.